[1112] Super Poker II
- 时间限制: 5000 ms 内存限制: 65535 K
- 问题描述
-
I have a set of super poker cards, consisting of an infinite number of cards. For each positive composite integer p, there are exactly four cards whose value is p: Spade(S), Heart(H), Club(C) and Diamond(D). There are no cards of other values. By “composite integer”, we mean integers that have more than 2 divisors. For example, 6 is a composite integer, since it has 4 divisors: 1, 2, 3, 6; 7 is not a composite number, since 7 only has 2 divisors: 1 and 7. Note that 1 is not composite (it has only 1 divisor).
Given a positive integer n, how many ways can you pick up exactly one card from each suit (i.e. exactly one spade card, one heart card, one club card and one diamond card), so that the card values sum to n? For example, if n=24, one way is 4S+6H+4C+10D, shown below:
Unfortunately, some of the cards are lost, but this makes the problem more interesting. To further make the problem even more interesting (and challenging!), I’ll give you two other positive integers a and b, and you need to find out all the answers for n=a, n=a+1, …, n=b.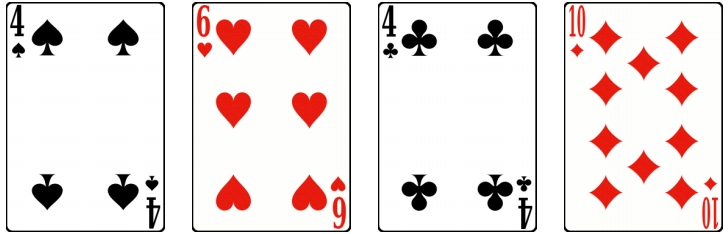
- 输入
-
The input contains at most 25 test cases. Each test case begins with 3 integers a, b and c, where c is the number of lost cards. The next line contains c strings, representing the lost cards. Each card is formatted as valueS, valueH, valueC or valueD, where value is a composite integer. No two lost cards are the same. The input is terminated by a=b=c=0. There will be at most one test case where a=1, b=50,000 and c<=10,000. For other test cases, 1<=a<=b<=100, 0<=c<=10.
- 输出
-
For each test case, print b-a+1 integers, one in each line. Since the numbers might be large, you should output each integer modulo 1,000,000. Print a blank line after each test case.
- 样例输入
-
12 20 2 4S 6H 0 0 0
- 样例输出
-
0 0 0 0 0 0 1 0 3
- 提示
-
无
- 来源
-
The Seventh Hunan Collegiate Programming Contest
- 操作
-

