There is a strongly-connected graph (i.e. you can reach any node from any other node) with n nodes and m edges. I will choose some of the edges to make another strongly connected graph. Your task is to guess that graph. Too difficult, right? Don’t worry, you only need to guess k edges. If all the edges exist in my graph, you win. I promise that from all possible graphs, the answer will be chosen uniformly. The original graph will not have self-loops or duplicated edges .

You already have a guess, but you are a bit unsure. Why not write a program to calculate the probability you win? For example, if n=4, m=5, the original graph has 5 edges: 1->2, 2->3, 3->4, 4->1, 1->3, there are only two possible answers:

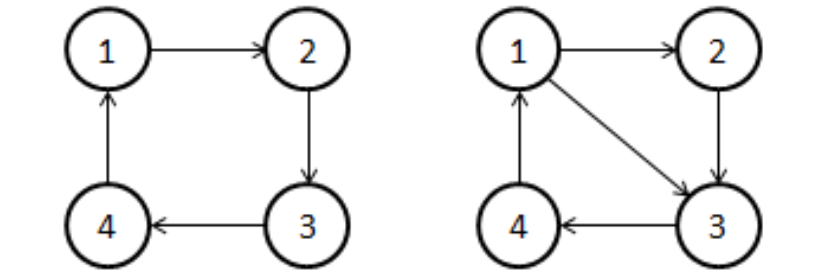
If k=2, the best way is to guess edge 1->2 and 2->3 (or 1->2 and 3->4 etc.) which will guarantee a win. But if you would like to risk by guessing edges 1->3 and 2->3, the probability you win is 0.5.